写在前面

AutoInt (Automatic Feature Interaction)，这是 2019 年发表在 CIKM 上的文章，这里面提出的模型，重点也是在特征交互上，而所用到的结构，就是大名鼎鼎的 transformer 结构了，也就是通过多头的自注意力机制来显示的构造高阶特征，有效的提升了模型的效果。所以这个模型的提出动机比较简单，和 xdeepFM 这种其实是一样的，就是针对目前很多浅层模型无法学习高阶的交互， 而 DNN 模型能学习高阶交互，但确是隐性学习，缺乏可解释性，并不知道好不好使。而 transformer 的话，我们知道， 有着天然的全局意识，在 NLP 里面的话，各个词通过多头的自注意力机制，就能够使得各个词从不同的子空间中学习到与其它各个词的相关性，汇聚其它各个词的信息。 而放到推荐系统领域，同样也是这个道理，无非是把词换成了这里的离散特征而已， 而如果通过多个这样的交叉块堆积，就能学习到任意高阶的交互啦。这其实就是本篇文章的思想核心。

AutoInt 模型的理论及论文细节

动机和原理

这篇文章的前言部分依然是说目前模型的不足，以引出模型的动机所在， 简单的来讲，就是两句话：

1. 浅层的模型会受到交叉阶数的限制，没法完成高阶交叉
2. 深层模型的 DNN 在学习高阶隐性交叉的效果并不是很好， 且不具有可解释性

于是乎：

那么是如何做到的呢？ 引入了 transformer， 做成了一个特征交互层， 原理如下：

AutoInt 模型的前向过程梳理

下面看下 AutoInt 模型的结构了，并不是很复杂

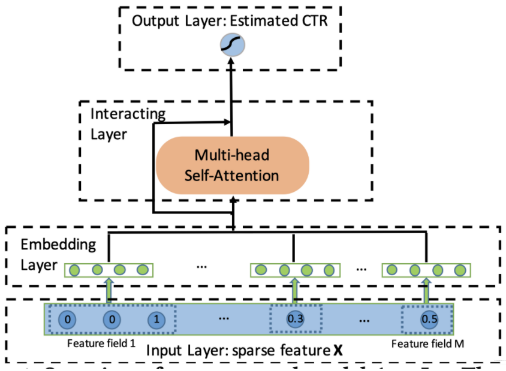
Input Layer

输入层这里， 用到的特征主要是离散型特征和连续性特征， 这里不管是哪一类特征，都会过 embedding 层转成低维稠密的向量，是的， 连续性特征，这里并没有经过分桶离散化，而是直接走 embedding。这个是怎么做到的呢？就是就是类似于预训练时候的思路，先通过 item_id 把连续型特征与类别特征关联起来，最简单的，就是把 item_id 拿过来，过完 embedding 层取出对应的 embedding 之后，再乘上连续值即可， 所以这个连续值事先一定要是归一化的。 当然，这个玩法，我也是第一次见。 学习到了， 所以模型整体的输入如下：

$$\mathbf{x}=[{\mathbf{x}}_1;{\mathbf{x}}_2;\dots ;{\mathbf{x}}_{\mathbf{M}}]$$

这里的$M$ 表示特征的个数，$X_1,X_2$ 这是离散型特征， one-hot 的形式， 而$X_M$ 在这里是连续性特征。过 embedding 层的细节应该是我上面说的那样。

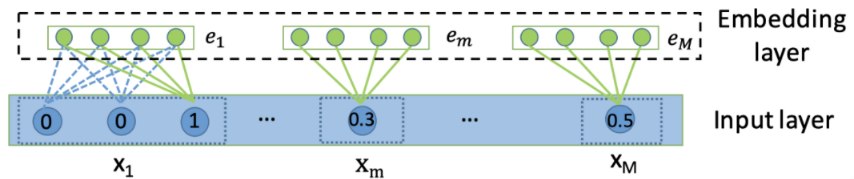
Embedding Layer

embedding 层的作用是把高维稀疏的特征转成低维稠密， 离散型的特征一般是取出对应的 embedding 向量即可， 具体计算是这样：

$${\mathbf{e}}_{\mathbf{i}}={\mathbf{V}}_{\mathbf{i}}{\mathbf{x}}_{\mathbf{i}}$$

对于第$i$ 个离散特征，直接第$i$ 个嵌入矩阵$V_i$ 乘 one-hot 向量就取出了对应位置的 embedding。 当然，如果输入的时候不是个 one-hot， 而是个 multi-hot 的形式，那么对应的 embedding 输出是各个 embedding 求平均得到的。

$${\mathbf{e}}_{\mathbf{i}}=\frac{1}{q}{\mathbf{V}}_{\mathbf{i}}{\mathbf{x}}_{\mathbf{i}}$$

比如， 推荐里面用户的历史行为 item。过去点击了多个 item，最终的输出就是这多个 item 的 embedding 求平均。 而对于连续特征， 我上面说的那样， 也是过一个 embedding 矩阵取相应的 embedding， 不过，最后要乘一个连续值

$${\mathbf{e}}_{\mathbf{m}}={\mathbf{v}}_{\mathbf{m}}{x}_m$$

这样，不管是连续特征，离散特征还是变长的离散特征，经过 embedding 之后，都能得到等长的 embedding 向量。 我们把这个向量拼接到一块，就得到了交互层的输入。

Interacting Layer

这个是本篇论文的核心了，其实这里说的就是 transformer 块的前向传播过程，所以这里我就直接用比较白话的语言简述过程了，不按照论文中的顺序展开了。

通过 embedding 层， 我们会得到 M 个向量$e_1,...e_M$，假设向量的维度是$d$ 维， 那么这个就是一个$d\times M$ 的矩阵， 我们定一个符号$X$。 接下来我们基于这个矩阵$X$，做三次变换，也就是分别乘以三个矩阵$W_k^{(h)},W_q^{(h)},W_v^{(h)}$， 这三个矩阵的维度是$d^{\prime }\times d$ 的话， 那么我们就会得到三个结果：

$$\begin{gathered} Q^{(h)}=W_q^{(h)}\times X \\ {K}^{(h)}=W_k^{(h)}\times X \\ {V}^{(h)}=W_v^{(h)}\times X \end{gathered}$$

这三个矩阵都是$d^{\prime }\times M$ 的。这其实就完成了一个 Head 的操作。所谓的自注意力， 就是$X$ 通过三次变换得到的结果之间，通过交互得到相关性，并通过相关性进行加权汇总，全是$X$ 自发的。 那么是怎么做到的呢？首先， 先进行这样的操作：

$$Score(Q^h,K^h)=Q^h\times {K^h}^T$$

这个结果得到的是一个$d^{\prime }\times d^{\prime }$ 的矩阵， 那么这个操作到底是做了一个什么事情呢？

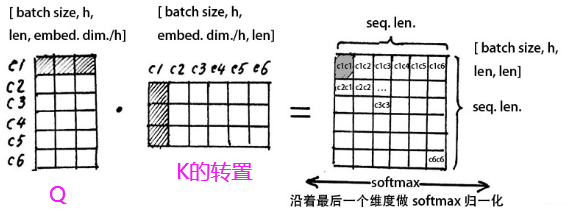
假设这里的$c_1..c_6$ 是我们的 6 个特征， 而每一行代表每个特征的 embedding 向量，这样两个矩阵相乘，相当于得到了当前特征与其它特征两两之间的內积值， 而內积可以表示两个向量之间的相似程度。所以得到的结果每一行，就代表当前这个特征与其它特征的相似性程度。

接下来，我们对$Score(Q^h,K^h)$， 在最后一个维度上进行 softmax，就根据相似性得到了权重信息，这其实就是把相似性分数归一化到了 0-1 之间

$$Attention(Q^h,K^h)=Softmax(Score(Q^h,K^h))$$

接下来， 我们再进行这样的一步操作

$$E^{(h)}=Attention(Q^h,K^h)\times V$$

这样就得到了$d^{\prime }\times M$ 的矩阵$E$， 这步操作，其实就是一个加权汇总的过程， 对于每个特征， 先求与其它特征的相似度，然后得到一个权重，再回乘到各自的特征向量再求和。 只不过这里的特征是经过了一次线性变化的过程，降维到了$d^{\prime }$。

上面是我从矩阵的角度又过了一遍， 这个是直接针对所有的特征向量一部到位。 论文里面的从单个特征的角度去描述的，只说了一个矩阵向量过多头注意力的操作。

$$\begin{gathered} \begin{array}{c}{\alpha }_{\mathbf{m},\mathbf{k}}^{(\mathbf{h})}=\frac{\exp \left({\psi }^{(h)}({\mathbf{e}}_{\mathbf{m}},{\mathbf{e}}_{\mathbf{k}})\right)}{\sum _{l=1}^M\exp \left({\psi }^{(h)}({\mathbf{e}}_{\mathbf{m}},{\mathbf{e}}_1)\right)}\\ {\psi }^{(h)}({\mathbf{e}}_{\mathbf{m}},{\mathbf{e}}_{\mathbf{k}})=⟨{\mathbf{W}}_{\text{Query }}^{(\mathbf{h})}{\mathbf{e}}_{\mathbf{m}},{\mathbf{W}}_{\text{Key }}^{(\mathbf{h})}{\mathbf{e}}_{\mathbf{k}}⟩\end{array} \\ {\tilde{\mathbf{e}}}_{\mathrm{m}}^{(\mathbf{h})}=\sum _{k=1}^M{\alpha }_{\mathbf{m},\mathbf{k}}^{(\mathbf{h})}\left({\mathbf{W}}_{\text{Value }}^{(\mathbf{h})}{\mathbf{e}}_{\mathbf{k}}\right) \end{gathered}$$

这里会更好懂一些， 就是相当于上面矩阵的每一行操作拆开了， 首先，整个拼接起来的 embedding 矩阵还是过三个参数矩阵得到$Q,K,V$， 然后是每一行单独操作的方式，对于某个特征向量$e_k$，与其它的特征两两內积得到权重，然后在 softmax，回乘到对应向量，然后进行求和就得到了融合其它特征信息的新向量。 具体过程如图：

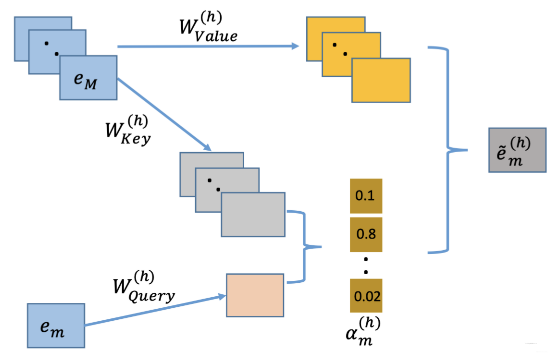
上面的过程是用了一个头，理解的话就类似于从一个角度去看特征之间的相关关系，用论文里面的话讲，这是从一个子空间去看， 如果是想从多个角度看，这里可以用多个头，即换不同的矩阵$W_q,W_k,W_v$ 得到不同的$Q,K,V$ 然后得到不同的$e_m$， 每个$e_m$ 是$d^{\prime }\times 1$ 的。

然后，多个头的结果 concat 起来

$${\tilde{\mathbf{e}}}_{\mathrm{m}}={\tilde{\mathbf{e}}}_{\mathrm{m}}^{(1)}\oplus {\tilde{\mathbf{e}}}_{\mathrm{m}}^{(2)}\oplus \cdots \oplus {\tilde{\mathbf{e}}}_{\mathbf{m}}^{(\mathbf{H})}$$

这是一个$d^{\prime }\times H$ 的向量， 假设有$H$ 个头。

接下来， 过一个残差网络层，这是为了保留原始的特征信息

$${\mathbf{e}}_{\mathbf{m}}^{\mathrm{Res}}=\mathrm{ReL}U({\tilde{\mathbf{e}}}_{\mathbf{m}}+{\mathbf{W}}_{\text{Res }}{\mathbf{e}}_{\mathbf{m}})$$

这里的$e_m$ 是$d\times 1$ 的向量， $W_{Res}$ 是$d^{\prime }H\times d$ 的矩阵， 最后得到的$e_m^{Res}$ 是$d^{\prime }H\times 1$ 的向量， 这是其中的一个特征，如果是$M$ 个特征堆叠的话，最终就是$d^{\prime }HM\times 1$ 的矩阵， 这个就是 Interacting Layer 的结果输出。

Output Layer

输出层就非常简单了，加一层全连接映射出输出值即可：

$$\hat{y}=\sigma ({\mathbf{w}}^{\mathrm{T}}({\mathbf{e}}_1^{\mathbf{R}\mathbf{e}\mathbf{s}}\oplus {\mathbf{e}}_2^{\mathbf{R}\mathbf{e}\mathbf{s}}\oplus \cdots \oplus {\mathbf{e}}_{\mathbf{M}}^{\text{Res }})+b)$$

这里的$W$ 是$d^{\prime }HM\times 1$ 的， 这样最终得到的是一个概率值了， 接下来交叉熵损失更新模型参数即可。

AutoInt 的前向传播过程梳理完毕。

AutoInt 的分析

这里论文里面分析了为啥 AutoInt 能建模任意的高阶交互以及时间复杂度和空间复杂度的分析。我们一一来看。

关于建模任意的高阶交互， 我们这里拿一个 transformer 块看下， 对于一个 transformer 块， 我们发现特征之间完成了一个 2 阶的交互过程，得到的输出里面我们还保留着 1 阶的原始特征。

那么再经过一个 transformer 块呢？ 这里面就会有 2 阶和 1 阶的交互了， 也就是会得到 3 阶的交互信息。而此时的输出，会保留着第一个 transformer 的输出信息特征。再过一个 transformer 块的话，就会用 4 阶的信息交互信息， 其实就相当于， 第$n$ 个 transformer 里面会建模出$n+1$ 阶交互来， 这个与 CrossNet 其实有异曲同工之妙的，无法是中间交互时的方式不一样。 前者是 bit-wise 级别的交互，而后者是 vector-wise 的交互。

所以， AutoInt 是可以建模任意高阶特征的交互的，并且这种交互还是显性。

关于时间复杂度和空间复杂度，空间复杂度是$O(Ld{d}^{\prime }H)$ 级别的， 这个也很好理解，看参数量即可， 3 个 W 矩阵， H 个 head，再假设 L 个 transformer 块的话，参数量就达到这了。 时间复杂度的话是$O(MH{d}^{\prime }(M+d))$ 的，论文说如果 d 和 d' 很小的话，其实这个模型不算复杂。

3.4 更多细节

这里整理下实验部分的细节，主要是对于一些超参的实验设置，在实验里面，作者首先指出了 logloss 下降多少算是有效呢？

It is noticeable that a slightly higher AUC or lower Logloss at 0.001-level is regarded significant for CTR prediction task, which has also been pointed out in existing works

这个和在 fibinet 中 auc 说的意思差不多。

在这一块，作者还写到了几个观点：

1. NFM use the deep neural network as a core component to learning high-order feature interactions, they do not guarantee improvement over FM and AFM.
2. AFM 准确的说是二阶显性交互基础上加了交互重要性选择的操作， 这里应该是没有在上面加全连接
3. xdeepFM 这种 CIN 网络，在实际场景中非常难部署，不实用
4. AutoInt 的交互层 2-3 层差不多， embedding 维度 16-24
5. 在 AutoInt 上面加 2-3 层的全连接会有点提升，但是提升效果并不是很大

所以感觉 AutoInt 这篇 paper 更大的价值，在于给了我们一种特征高阶显性交叉与特征选择性的思路，就是 transformer 在这里起的功效。所以后面用的时候， 更多的应该考虑如何用这种思路或者这个交互模块，而不是直接搬模型。

AutoInt 模型的简单复现及结构解释

经过上面的分析， AutoInt 模型的核心其实还是 Transformer，所以代码部分呢？ 主要还是 Transformer 的实现过程， 这个之前在整理 DSIN 的时候也整理过，由于 Transformer 特别重要，所以这里再重新复习一遍， 依然是基于 Deepctr，写成一个简版的形式。

def AutoInt(linear_feature_columns, dnn_feature_columns, att_layer_num=3, att_embedding_size=8, att_head_num=2, att_res=True):
    """
    :param att_layer_num: transformer块的数量，一个transformer块里面是自注意力计算 + 残差计算
    :param att_embedding_size:  文章里面的d', 自注意力时候的att的维度
    :param att_head_num: 头的数量或者自注意力子空间的数量
    :param att_res: 是否使用残差网络
    """
    # 构建输入层，即所有特征对应的Input()层，这里使用字典的形式返回，方便后续构建模型
    dense_input_dict, sparse_input_dict = build_input_layers(linear_feature_columns+dnn_feature_columns)
    
    # 构建模型的输入层，模型的输入层不能是字典的形式，应该将字典的形式转换成列表的形式
    # 注意：这里实际的输入预Input层对应，是通过模型输入时候的字典数据的key与对应name的Input层
    input_layers = list(dense_input_dict.values()) + list(sparse_input_dict.values())
    
    # 线性部分的计算逻辑 -- linear
    linear_logits = get_linear_logits(dense_input_dict, sparse_input_dict, linear_feature_columns)
    
    # 构建维度为k的embedding层，这里使用字典的形式返回，方便后面搭建模型
    # 线性层和dnn层统一的embedding层
    embedding_layer_dict = build_embedding_layers(linear_feature_columns+dnn_feature_columns, sparse_input_dict, is_linear=False)
    
    # 构造self-att的输入
    att_sparse_kd_embed = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=False)
    att_input = Concatenate(axis=1)(att_sparse_kd_embed)   # (None, field_num, embed_num)
    
    # 下面的循环，就是transformer的前向传播，多个transformer块的计算逻辑
    for _ in range(att_layer_num):
        att_input = InteractingLayer(att_embedding_size, att_head_num, att_res)(att_input)
    att_output = Flatten()(att_input)
    att_logits = Dense(1)(att_output)
    
    # DNN侧的计算逻辑 -- Deep
    # 将dnn_feature_columns里面的连续特征筛选出来，并把相应的Input层拼接到一块
    dnn_dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), dnn_feature_columns)) if dnn_feature_columns else []
    dnn_dense_feature_columns = [fc.name for fc in dnn_dense_feature_columns]
    dnn_concat_dense_inputs = Concatenate(axis=1)([dense_input_dict[col] for col in dnn_dense_feature_columns])
    
    # 将dnn_feature_columns里面的离散特征筛选出来，相应的embedding层拼接到一块
    dnn_sparse_kd_embed = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=True)
    dnn_concat_sparse_kd_embed = Concatenate(axis=1)(dnn_sparse_kd_embed)
    
    # DNN层的输入和输出
    dnn_input = Concatenate(axis=1)([dnn_concat_dense_inputs, dnn_concat_sparse_kd_embed, att_output])
    dnn_out = get_dnn_output(dnn_input)
    dnn_logits = Dense(1)(dnn_out)
     
    # 三边的结果stack
    stack_output = Add()([linear_logits, dnn_logits])
    
    # 输出层
    output_layer = Dense(1, activation='sigmoid')(stack_output)
    
    model = Model(input_layers, output_layer)
    
    return model

这里由于大部分都是之前见过的模块，唯一改变的地方，就是加了一个 InteractingLayer ， 这个是一个 transformer 块，在这里面实现特征交互。而这个的结果输出，最终和 DNN 的输出结合到一起了。 而这个层，主要就是一个 transformer 块的前向传播过程。这应该算是最简单的一个版本了:

class InteractingLayer(Layer):
    """A layer user in AutoInt that model the correction between different feature fields by multi-head self-att mechanism
        input: 3维张量, (none, field_num, embedding_size)
        output: 3维张量, (none, field_num, att_embedding_size * head_num)
    """
    def __init__(self, att_embedding_size=8, head_num=2, use_res=True, seed=2021):
        super(InteractingLayer, self).__init__()
        self.att_embedding_size = att_embedding_size
        self.head_num = head_num
        self.use_res = use_res
        self.seed = seed
        
    
    def build(self, input_shape):
        embedding_size = int(input_shape[-1])
        
        # 定义三个矩阵Wq, Wk, Wv
        self.W_query = self.add_weight(name="query", shape=[embedding_size, self.att_embedding_size * self.head_num],
                                        dtype=tf.float32, initializer=tf.keras.initializers.TruncatedNormal(seed=self.seed))
        self.W_key = self.add_weight(name="key", shape=[embedding_size, self.att_embedding_size * self.head_num], 
                                     dtype=tf.float32, initializer=tf.keras.initializers.TruncatedNormal(seed=self.seed+1))
        self.W_value = self.add_weight(name="value", shape=[embedding_size, self.att_embedding_size * self.head_num],
                                      dtype=tf.float32, initializer=tf.keras.initializers.TruncatedNormal(seed=self.seed+2))
        
        if self.use_res:
            self.W_res = self.add_weight(name="res", shape=[embedding_size, self.att_embedding_size * self.head_num],
                                        dtype=tf.float32, initializer=tf.keras.initializers.TruncatedNormal(seed=self.seed+3))
        
        super(InteractingLayer, self).build(input_shape)
    
    def call(self, inputs):
        # inputs (none, field_nums, embed_num)
        
        querys = tf.tensordot(inputs, self.W_query, axes=(-1, 0))   # (None, field_nums, att_emb_size*head_num)
        keys = tf.tensordot(inputs, self.W_key, axes=(-1, 0))
        values = tf.tensordot(inputs, self.W_value, axes=(-1, 0))
        
        # 多头注意力计算 按照头分开  (head_num, None, field_nums, att_embed_size)
        querys = tf.stack(tf.split(querys, self.head_num, axis=2))
        keys = tf.stack(tf.split(keys, self.head_num, axis=2))
        values = tf.stack(tf.split(values, self.head_num, axis=2))
        
        # Q * K, key的后两维转置，然后再矩阵乘法 
        inner_product = tf.matmul(querys, keys, transpose_b=True)    # (head_num, None, field_nums, field_nums)
        normal_att_scores = tf.nn.softmax(inner_product, axis=-1)
        
        result = tf.matmul(normal_att_scores, values)   # (head_num, None, field_nums, att_embed_size)
        result = tf.concat(tf.split(result, self.head_num, ), axis=-1)  # (1, None, field_nums, att_emb_size*head_num)
        result = tf.squeeze(result, axis=0)  # (None, field_num, att_emb_size*head_num)
        
        if self.use_res:
            result += tf.tensordot(inputs, self.W_res, axes=(-1, 0))
        
        result = tf.nn.relu(result)
        
        return result

这就是一个 Transformer 块做的事情，这里只说两个小细节:

• 第一个是参数初始化那个地方， 后面的 seed 一定要指明出参数来，我第一次写的时候， 没有用 seed=，结果导致训练有问题。
• 第二个就是这里自注意力机制计算的时候，这里的多头计算处理方式， 把多个头分开，采用堆叠的方式进行计算 (堆叠到第一个维度上去了)。只有这样才能使得每个头与每个头之间的自注意力运算是独立不影响的。如果不这么做的话，最后得到的结果会含有当前单词在这个头和另一个单词在另一个头上的关联，这是不合理的。

OK， 这就是 AutoInt 比较核心的部分了，当然，上面自注意部分的输出结果与 DNN 或者 Wide 部分结合也不一定非得这么一种形式，也可以灵活多变，具体得结合着场景来。详细代码依然是看后面的 GitHub 啦。

总结

这篇文章整理了 AutoInt 模型，这个模型的重点是引入了 transformer 来实现特征之间的高阶显性交互， 而 transformer 的魅力就是多头的注意力机制，相当于在多个子空间中， 根据不同的相关性策略去让特征交互然后融合，在这个交互过程中，特征之间计算相关性得到权重，并加权汇总，使得最终每个特征上都有了其它特征的信息，且其它特征的信息重要性还有了权重标识。 这个过程的自注意力计算以及汇总是一个自动的过程，这是很 powerful 的。

所以这篇文章的重要意义是又给我们传授了一个特征交互时候的新思路，就是 transformer 的多头注意力机制。

在整理 transformer 交互层的时候， 这里忽然想起了和一个同学的讨论， 顺便记在这里吧，就是：

自注意力里面的 Q,K 能用一个吗？ 也就是类似于只用 Q， 算注意力的时候，直接$Q{Q}^T$， 得到的矩阵维度和原来的是一样的，并且在参数量上，由于去掉了$w_k$ 矩阵， 也会有所减少。

关于这个问题， 我目前没有尝试用同一个的效果，但总感觉是违背了当时设计自注意力的初衷，最直接的一个结论，就是这里如果直接$Q{Q}^T$，那么得到的注意力矩阵是一个对称的矩阵， 这在汇总信息的时候可能会出现问题。 因为这基于了一个假设就是 A 特征对于 B 特征的重要性，和 B 特征对于 A 的重要性是一致的， 这个显然是不太符合常规的。 比如 "学历" 这个特征和 "职业" 这个特征， 对于计算机行业，高中生和研究生或许都可以做， 但是对于金融类的行业， 对学历就有着很高的要求。 这就说明对于职业这个特征， 学历特征对其影响很大。 而如果是看学历的话，研究生学历或许可以入计算机，也可以入金融， 可能职业特征对学历的影响就不是那么明显。 也就是学历对于职业的重要性可能会比职业对于学历的重要性要大。 所以我感觉直接用同一个矩阵，在表达能力上会受到限制。当然，是自己的看法哈， 这个问题也欢迎一块讨论呀！

参考资料：

• AutoInt: Automatic Feature Interaction Learning via Self-Attentive Neural Networks
• AutoInt：基于 Multi-Head Self-Attention 构造高阶特征