PNN
动机
在特征交叉的相关模型中 FM, FFM 都证明了特征交叉的重要性,FNN 将神经网络的高阶隐式交叉加到了 FM 的二阶特征交叉上,一定程度上说明了 DNN 做特征交叉的有效性。但是对于 DNN 这种 “add” 操作的特征交叉并不能充分挖掘类别特征的交叉效果。PNN 虽然也用了 DNN 来对特征进行交叉组合,但是并不是直接将低阶特征放入 DNN 中,而是设计了 Product 层先对低阶特征进行充分的交叉组合之后再送入到 DNN 中去。
PNN 模型其实是对 IPNN 和 OPNN 的总称,两者分别对应的是不同的 Product 实现方法,前者采用的是 inner product,后者采用的是 outer product。在 PNN 的算法方面,比较重要的部分就是 Product Layer 的简化实现方法,需要在数学和代码上都能够比较深入的理解。
模型的结构及原理
在学习 PNN 模型之前,应当对于 DNN 结构具有一定的了解,同时已经学习过了前面的章节。
PNN 模型的整体架构如下图所示:
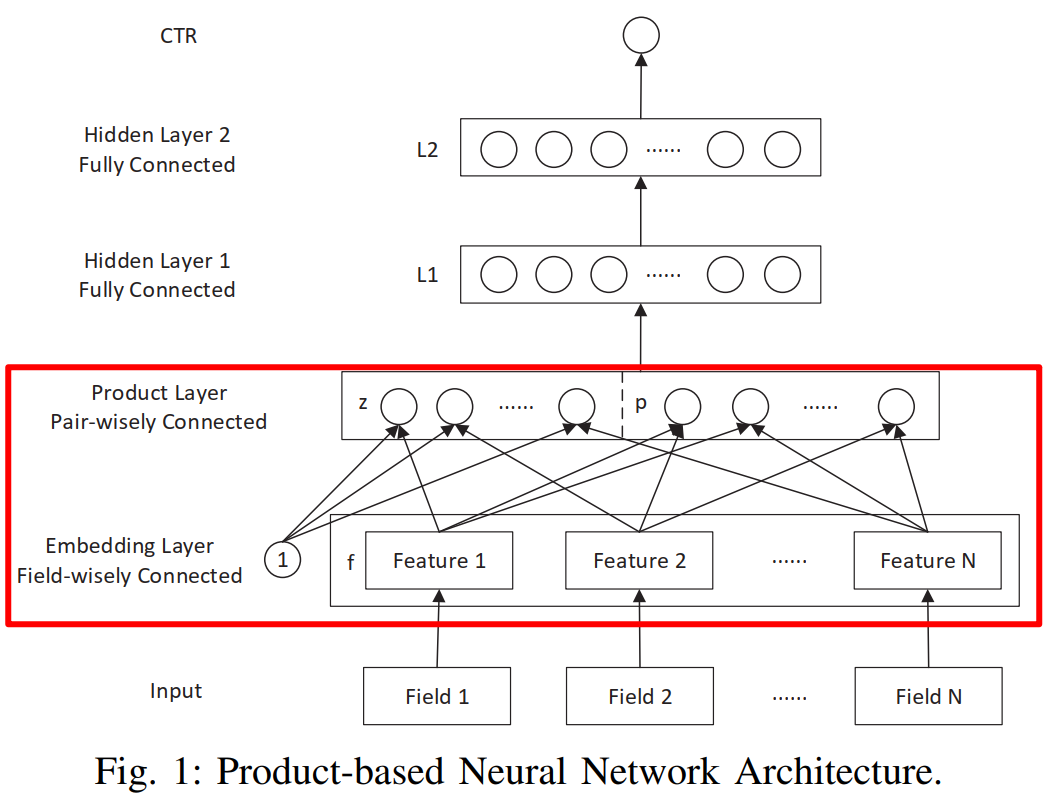
一共分为五层,其中除了 Product Layer 别的 layer 都是比较常规的处理方法,均可以从前面的章节进一步了解。模型中最重要的部分就是通过 Product 层对 embedding 特征进行交叉组合,也就是上图中红框所显示的部分。
Product 层主要有线性部分和非线性部分组成,分别用
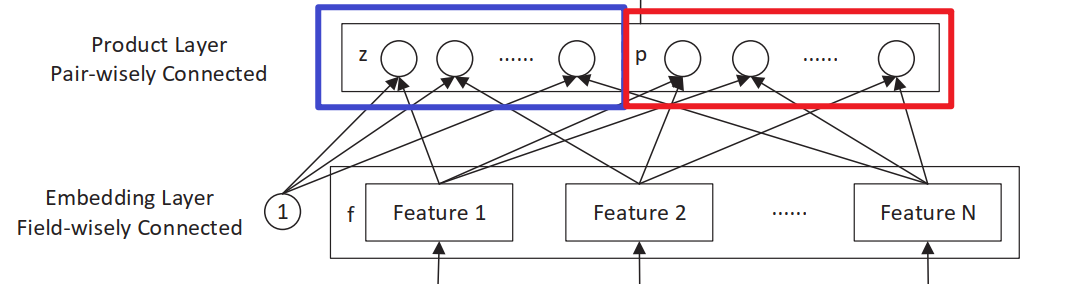
- 线性模块,一阶特征 (未经过显示特征交叉处理),对应论文中的
- 非线性模块,高阶特征 (经过显示特征交叉处理),对应论文中的
线性部分
先来解释一下
总之这一波操作就是将所有的 embedding 向量中的所有元素都乘以一个矩阵的对应元素,最后相加即可,这一部分比较简单 (N 表示的是特征的数量,M 表示的是所有特征转化为 embedding 之后维度,也就是 N*emb_dim)
Product Layer
非线性部分
上面介绍了线性部分
从上述公式中可以发现,
IPNN
使用内积实现特征交叉就和 FM 是类似的 (两两向量计算内积),下面将向量内积操作表示如下表达式
将内积的表达式带入
上面就提到了这里使用的内积是计算两两特征之间的内积,然而向量 a 和向量 b 的内积与向量 b 和向量 a 的内积是相同的,其实是没必要计算的,看一下下面 FM 的计算公式:
也就是说计算的内积矩阵
所以优化后的
这里为了好理解不做过多的解释,其实这里对于矩阵分解省略了一些细节,感兴趣的可以去看原文,最后模型实现的时候就是基于上面的这个公式计算的(给出的代码也是基于优化之后的实现)。
OPNN
使用外积实现相比于使用内积实现,唯一的区别就是使用向量的外积来计算矩阵
从外积公式可以发现两个向量的外积得到的是一个矩阵,与上面介绍的内积计算不太相同,内积得到的是一个数值。内积实现的 Product 层是将计算得到的内积矩阵,乘以一个与其大小一样的权重矩阵,然后求和,按照这个思路的话,通过外积得到的
需要注意的是此时的
需要注意,这里新定义的外积计算与传统的外积计算时不等价的,这里是为了优化计算效率重新定义的计算方式,从公式中可以看出,相当于先将原来的 embedding 向量在特征维度上先求和,变成一个向量之后再计算外积。加入原 embedding 向量表示为
最终的计算方式和
虽然叠加概念的引入可以降低计算开销,但是中间的精度损失也是很大的,性能与精度之间的 tradeoff
代码实现
代码实现的整体逻辑比较简单,就是对类别特征进行 embedding 编码,然后通过 embedding 特征计算
def PNN(dnn_feature_columns, inner=True, outer=True):
# 构建输入层,即所有特征对应的Input()层,这里使用字典的形式返回,方便后续构建模型
_, sparse_input_dict = build_input_layers(dnn_feature_columns)
# 构建模型的输入层,模型的输入层不能是字典的形式,应该将字典的形式转换成列表的形式
# 注意:这里实际的输入与Input()层的对应,是通过模型输入时候的字典数据的key与对应name的Input层
input_layers = list(sparse_input_dict.values())
# 构建维度为k的embedding层,这里使用字典的形式返回,方便后面搭建模型
embedding_layer_dict = build_embedding_layers(dnn_feature_columns, sparse_input_dict, is_linear=False)
sparse_embed_list = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=False)
dnn_inputs = ProductLayer(units=32, use_inner=True, use_outer=True)(sparse_embed_list)
# 输入到dnn中,需要提前定义需要几个残差块
output_layer = get_dnn_logits(dnn_inputs)
model = Model(input_layers, output_layer)
return model2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
PNN 的难点就是 Product 层的实现,下面是 Product 层实现的代码,代码中是使用优化之后
class ProductLayer(Layer):
def __init__(self, units, use_inner=True, use_outer=False):
super(ProductLayer, self).__init__()
self.use_inner = use_inner
self.use_outer = use_outer
self.units = units # 指的是原文中D1的大小
def build(self, input_shape):
# 需要注意input_shape也是一个列表,并且里面的每一个元素都是TensorShape类型,
# 需要将其转换成list然后才能参与数值计算,不然类型容易错
# input_shape[0] : feat_nums x embed_dims
self.feat_nums = len(input_shape)
self.embed_dims = input_shape[0].as_list()[-1]
flatten_dims = self.feat_nums * self.embed_dims
# Linear signals weight, 这部分是用于产生Z的权重,因为这里需要计算的是两个元素对应元素乘积然后再相加
# 等价于先把矩阵拉成一维,然后相乘再相加
self.linear_w = self.add_weight(name='linear_w', shape=(flatten_dims, self.units), initializer='glorot_normal')
# inner product weight
if self.use_inner:
# 优化之后的内积权重是未优化时的一个分解矩阵,未优化时的矩阵大小为:D x N x N
# 优化后的内积权重大小为:D x N
self.inner_w = self.add_weight(name='inner_w', shape=(self.units, self.feat_nums), initializer='glorot_normal')
if self.use_outer:
# 优化之后的外积权重大小为:D x embed_dim x embed_dim, 因为计算外积的时候在特征维度通过求和的方式进行了压缩
self.outer_w = self.add_weight(name='outer_w', shape=(self.units, self.embed_dims, self.embed_dims), initializer='glorot_normal')
def call(self, inputs):
# inputs是一个列表
# 先将所有的embedding拼接起来计算线性信号部分的输出
concat_embed = Concatenate(axis=1)(inputs) # B x feat_nums x embed_dims
# 将两个矩阵都拉成二维的,然后通过矩阵相乘得到最终的结果
concat_embed_ = tf.reshape(concat_embed, shape=[-1, self.feat_nums * self.embed_dims])
lz = tf.matmul(concat_embed_, self.linear_w) # B x units
# inner
lp_list = []
if self.use_inner:
for i in range(self.units):
# 相当于给每一个特征向量都乘以一个权重
# self.inner_w[i] : (embed_dims, ) 添加一个维度变成 (embed_dims, 1)
# concat_embed: B x feat_nums x embed_dims; delta = B x feat_nums x embed_dims
delta = tf.multiply(concat_embed, tf.expand_dims(self.inner_w[i], axis=1))
# 在特征之间的维度上求和
delta = tf.reduce_sum(delta, axis=1) # B x embed_dims
# 最终在特征embedding维度上求二范数得到p
lp_list.append(tf.reduce_sum(tf.square(delta), axis=1, keepdims=True)) # B x 1
# outer
if self.use_outer:
# 外积的优化是将embedding矩阵,在特征间的维度上通过求和进行压缩
feat_sum = tf.reduce_sum(concat_embed, axis=1) # B x embed_dims
# 为了方便计算外积,将维度进行扩展
f1 = tf.expand_dims(feat_sum, axis=2) # B x embed_dims x 1
f2 = tf.expand_dims(feat_sum, axis=1) # B x 1 x embed_dims
# 求外积, a * a^T
product = tf.matmul(f1, f2) # B x embed_dims x embed_dims
# 将product与外积权重矩阵对应元素相乘再相加
for i in range(self.units):
lpi = tf.multiply(product, self.outer_w[i]) # B x embed_dims x embed_dims
# 将后面两个维度进行求和,需要注意的是,每使用一次reduce_sum就会减少一个维度
lpi = tf.reduce_sum(lpi, axis=[1, 2]) # B
# 添加一个维度便于特征拼接
lpi = tf.expand_dims(lpi, axis=1) # B x 1
lp_list.append(lpi)
# 将所有交叉特征拼接到一起
lp = Concatenate(axis=1)(lp_list)
# 将lz和lp拼接到一起
product_out = Concatenate(axis=1)([lz, lp])
return product_out2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
因为这个模型的整体实现框架比较简单,就不画实现的草图了,直接看模型搭建的函数即可,对于 PNN 重点需要理解 Product 的两种类型及不同的优化方式。
下面是一个通过 keras 画的模型结构图,为了更好的显示,类别特征都只是选择了一小部分,画图的代码也在 github 中。
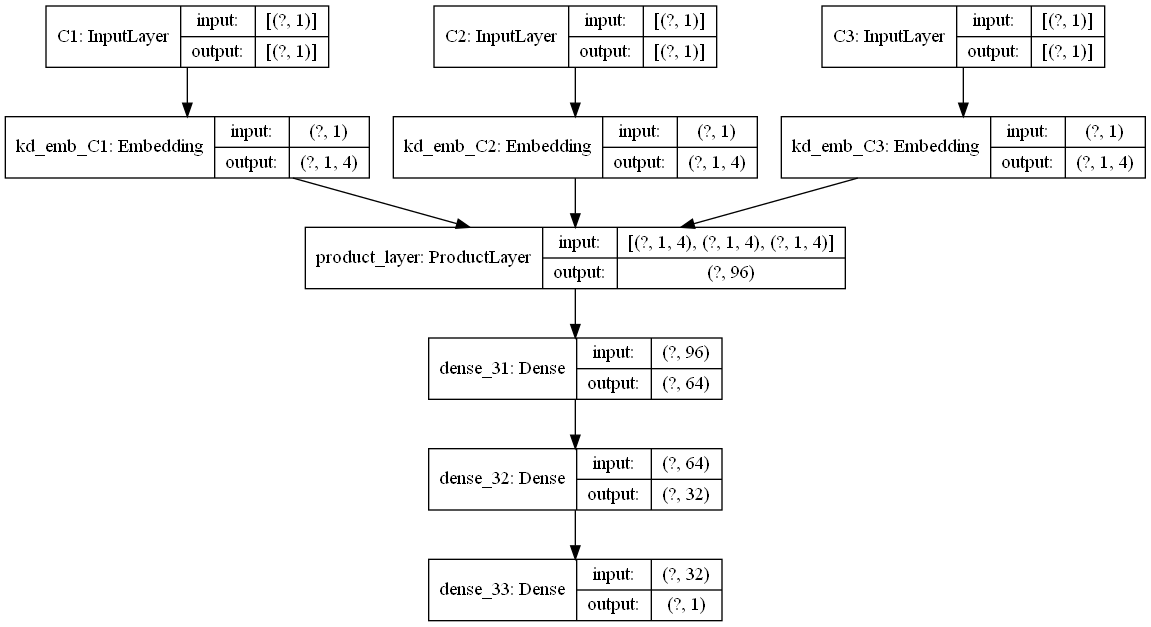
思考题
- 降低复杂度的具体策略与具体的 product 函数选择有关,IPNN 其实通过矩阵分解,“跳过” 了显式的 product 层,而 OPNN 则是直接在 product 层入手进行优化。看原文去理解优化的动机及细节。
参考文献