写在前面
xDeepFM (eXtreme DeepFM),这是 2018 年中科大联合微软在 KDD 上提出的一个模型,在 DeepFM 的前面加了一个 eXtreme,看这个名字,貌似是 DeepFM 的加强版,但当我仔细的读完原文之后才发现,如果论血缘关系,这个模型应该离着 DCN 更近一些,这个模型的改进出发点依然是如何更好的学习特征之间的高阶交互作用,从而挖掘更多的交互信息。而基于这样的动机,作者提出了又一个更 powerful 的网络来完成特征间的高阶显性交互 (DCN 的话是一个交叉网络), 这个网络叫做 CIN (Compressed Interaction Network),这个网络也是 xDeepFM 的亮点或者核心创新点了 (牛 x 的地方), 有了这个网络才使得这里的 "Deep" 变得名副其实。而 xDeepFM 的模型架构依然是 w&D 结构,更好的理解方式就是用这个 CIN 网络代替了 DCN 里面的 Cross Network, 这样使得该网络同时能够显性和隐性的学习特征的高阶交互 (显性由 CIN 完成,隐性由 DNN 完成)。 那么为啥需要同时学习特征的显性和隐性高阶交互呢? 为啥会用 CIN 代替 Cross Network 呢? CIN 到底有什么更加强大之处呢? xDeepFM 与之前的 DeepFM 以及 FM 的关系是怎样的呢? 这些问题都会在后面一一揭晓。
这篇文章的逻辑和前面一样,首先依然是介绍 xDeepFM 的理论部分和论文里面的细节,我觉得这篇文章的创新思路还是非常厉害的,也就是 CIN 的结构,在里面是会看到 RNN 和 CNN 的身影的,又会看到 Cross Network 的身影。所以这个结构我这次也是花了一些时间去理解,花了一些时间找解读文章看, 但讲真,解读文章真没有论文里面讲的清晰,所以我这次整理也是完全基于原论文加上我自己的理解进行解读。 当然,我水平有限,难免有理解不到位的地方,如果发现有错,也麻烦各位大佬帮我指出来呀。这样优秀的一个模型,不管是工业上还是面试里面,也是非常喜欢用或者考的内容,所以后面依然参考 deepctr 的代码,进行简化版的复现,重点看看 CIN 结构的实现过程。最后就是简单介绍和小总。
这篇文章依然比较长,首先是 CIN 结构本身可能比较难理解,前面需要一定的铺垫任务,比如一些概念 (显隐性交叉,bit-wise 和 vector-wise 等), 一些基础模型 (FM,FNN,PNN,DNN 等),DCN 的 Cross Network,有了这些铺垫后再理解 CIN 以及操作会简单些,而 CIN 本身运算也可能比较复杂,再加上里面时间复杂度和空间复杂度那块的分析,还有后面实验的各个小细节以最后论文还帮助我们串联了各种模型,我想在这篇文章中都整理一下。 再加上模型的复现内容,所以篇幅上还是会很长,各取所需吧还是哈哈。当然这篇文章的重点还是在 CIN,这个也是面试里面非常喜欢问的点。
xDeepFM? 我们需要先了解这些
简介与进化动机
再具体介绍 xDeepFM 之前,想先整理点铺垫的知识,也是以前的一些内容,是基于原论文的 Introduction 部分摘抄了一些,算是对前面内容的一些回顾吧,因为这段时间一直忙着找实习,也已经好久没有写这个系列的相关文章了。所以多少还是有点风格和知识上的遗忘哈哈。
首先是在推荐系统里面, 一般原始的特征很难让模型学习到隐藏在数据背后的规律,因为推荐系统中的原始特征往往非常稀疏,且维度非常高。所以如果想得到一个好的推荐系统,我们必须尽可能的制作更多的特征出来,而特征组合往往是比较好的方式,毕竟特征一般都不是独立存在的,那么特征究竟怎么组合呢? 这是一个比较值得研究的难题,并且好多学者在这上面也下足了工夫。 如果你说,特征组合是啥来? 不太清楚了呀,那么文章中这个例子正好能解决你的疑问

起初的时候,是人工特征组合,这个往往在作比赛的时候会遇到,就是特征工程里面自己进行某些特征的交叉与组合来生成新的特征。 这样的方式会有几个问题,作者在论文里面总结了:
- 一般需要一些经验和时间才会得到比较好的特征组合,也就是找这样的组合对于人来说有着非常高的要求,无脑组合不可取 --- 需要一定的经验,耗费大量的时间
- 由于推荐系统中数据的维度规模太大了,如果人工进行组合,根本就不太可能实现 --- 特征过多,无法全面顾及特征的组合
- 手工制作的特征也没有一定的泛化能力,而恰巧推荐系统中的数据往往又非常稀疏 --- 手工组合无泛化能力
所以,让模型自动的进行特征交叉组合探索成了推荐模型里面的比较重要的一个任务,还记得吗? 这个也是模型进化的方向之一,之所以从前面进行引出,是因为本质上这篇的主角 xDeepFM 也是从这个方向上进行的探索, 那么既然又探索,那也说明了前面模型在这方面还有一定的问题,那么我们就来再综合理一理。
FM 模型:这个模型能够自动学习特征之间的两两交叉,并且比较厉害的地方就是用特征的隐向量内积去表示两两交叉后特征的重要程度,这使得模型在学习交互信息的同时,也让模型有了一定的泛化能力。 But,这个模型也有缺点,首先一般是只能应付特征的两两交叉,再高阶一点的交叉虽然行,但计算复杂,并且作者在论文中提到了高阶交叉的 FM 模型是不管有用还是无用的交叉都建模,这往往会带来一定的噪声。
DNN 模型:这个非常熟悉了,深度学习到来之后,推荐模型的演化都朝着 DNN 的时代去了,原因之一就是因为 DNN 的多层神经网络可以比较出色的完成特征之间的高阶交互,只需要增加网络的层数,就可以轻松的学习交互,这是 DNN 的优势所在。 比较有代表的模型 PNN,DeepCrossing 模型等。 But, DNN 并不是非常可靠,有下面几个问题。
- 首先,DNN 的这种特征交互是隐性的,后面会具体说显隐性交互区别,但直观上理解,这种隐性交互我们是无法看到到底特征之间是怎么交互的,具体交互到了几阶,这些都是带有一定的不可解释性。
- 其次,DNN 是 bit-wise 层级的交叉,关于 bit-wise,后面会说,这种方式论文里面说一个 embedding 向量里面的各个元素也会相互影响, 这样我觉得在这里带来的一个问题就是可能会发生过拟合。 因为我们知道 embedding 向量的表示方法就是想从不同的角度去看待某个商品 (比如颜色,价格,质地等),当然 embedding 各个维度是无可解释性的,但我们还是希望这各个维度更加独立一点好,也就是相关性不那么大为妙,这样的话往往能更加表示出各个商品的区别来。 但如果这各个维度上的元素也互相影响了 (神经网络会把这个也学习进去), 那过拟合的风险会变大。当然,上面这个是我自己的感觉, 原作者只是给了这样一段:

也就是 DNN 是否能够真正的有效学习特征之间的高阶交互是个谜! 3. DNN 还存在的问题就是学习高阶交互或许是可能,但没法再兼顾低阶交互,也就是记忆能力,所以后面 w&D 架构在成为了主流架构。
Wide&Deep, DeepFM 模型:这两个模型是既有 DNN 的深度,也有 FM 或者传统模型的广度,兼顾记忆能力和泛化能力,也是后面的主流模型。但依然有不足之处,wide&Deep 的话不用多讲,首先逻辑回归 (宽度部分) 仍然需要人工特征交叉,而深度部分的高阶交叉又是一个谜。 DeepFM 的话是 FM 和 DNN 的组合,用 FM 替代了逻辑回归,这样至少是模型的自动交叉特征,结合了 FM 的二阶以及 DNN 的高阶交叉能力。 但如果 DNN 这块高度交叉是个谜的话,就有点玄乎了。
DCN 网络:这个模型也是 w&D 架构,不过宽度那部分使用了一个 Cross Network,这个网络的奇妙之处,就是扩展了 FM 这种只能显性交叉的二阶的模型, 通过交叉网络能真正的显性的进行特征间的高阶交叉。 具体结构后面还会在复习,毕竟这次的 xdeepFM 主要是在 Cross Network 的基础上进行的再升级,这也是为啥说论血缘关系,xdeepFM 离 DCN 更近一些的原因。那么 Cross network 有啥问题呢? 这个想放在后面的 2.4 去说了,这样能更好的引出本篇主角来。
通过上面的一个梳理,首先是回忆起了前面这几个模型的发展脉络, 其次差不多也能明白 xDeepFM 到底再干个什么事情了,或者要解决啥问题了,xDeepFM 其实简单的说,依然是研究如何自动的进行特征之间的交叉组合,以让模型学习的更好。 从上面这段梳理中,我们至少要得到 3 个重要信息:
- 推荐模型如何有效的学习特征的交叉组合信息是非常重要的, 而原始的人工特征交叉组合不可取,如何让模型自动的学习交叉组合信息就变得非常关键
- 有的模型 (FM) 可以显性的交叉特征, 但往往没法高阶,只能到二阶
- 有的模型 (DNN) 可以进行高阶的特征交互,但往往是以一种无法解释的方式 (隐性高阶交互),并且是 bit-wise 的形式,能不能真正的学习到高阶交互其实是个谜。
- 有的模型 (DCN) 探索了显性的高阶交叉特征,但仍然存在一些问题。
所以 xDeepFM 的改进动机来了: 更有效的高阶显性交叉特征 (CIN),更高的泛化能力 (vector-wise), 显性和隐性高阶特征的组合 (CIN+DNN), 这就是 xDeepFM 了, 而这里面的关键,就是 CIN 网络了。在这之前,还是先把准备工作做足。
Embedding Layer
这个是为了回顾一下,简单一说,我们拿到的数据往往会有连续型数据和离散型或者叫类别型数据之分。 如果是连续型数据,那个不用多说,一般会归一化或者标准化处理,当然还可能进行一定的非线性化操作,就算处理完了。 而类别型数据,一般需要先 LabelEncoder,转成类别型编码,然后再 one-hot 转成 0 或者 1 的编码格式。 比如论文里面的这个例子:

这样的数据往往是高维稀疏的,不利于模型的学习,所以往往在这样数据之后,加一个 embedding 层,把数据转成低维稠密的向量表示。 关于 embedding 的原理这里不说了,但这里要注意一个细节,就是如果某个特征每个样本只有一种取值,也就是 one-hot 里面只有一个地方是 1,比如前面 3 个 field。这时候,可以直接拿 1 所在位置的 embedding 当做此时类别特征的 embedding 向量。 但是如果某个特征域每个样本好多种取值,比如 interests 这个,有好几个 1 的这种,那么就拿到 1 所在位置的 embedding 向量之后求和来代表该类别特征的 embedding。这样,经过 embedding 层之后,我们得到的数据成下面这样了:
这个应该比较好理解,

bit-wise VS vector-wise
这是特征交互的两种方式,需要了解下,因为论文里面的 CIN 结构是在 vector-wise 上完成特征交互的, 这里拿从网上找到的一个例子来解释概念。
假设隐向量的维度是 3 维, 如果两个特征对应的向量分别是
- bit-wise = element-wise 在进行交互时,交互的形式类似于
- vector-wise 如果特征交互形式类似于
这个一直没弄明白后者为什么会比前者好,我也在讨论群里问过这个问题,下面是得到的一个伙伴的想法:

对于这个问题有想法的伙伴,也欢迎在下面评论,我自己的想法是 bit-wise 看上面的定义,仿佛是在元素的级别交叉,然后学习权重, 而 vector-wise 是在向量的级别交叉,然后学习统一权重,bit-wise 具体到了元素级别上,虽然可能学习的更加细致,但这样应该会增加过拟合的风险,失去一定的泛化能力,再联想作者在论文里面解释的 bit-wise:

更觉得这个想法会有一定的合理性,就想我在 DNN 那里解释这个一样,把细节学的太细,就看不到整体了,佛曰:着相了哈哈。如果再联想下 FM 的设计初衷,FM 是一个 vector-wise 的模型,它进行了显性的二阶特征交叉,却是 embedding 级别的交互,这样的好处是有一定的泛化能力到看不见的特征交互。 emmm, 我在后面整理 Cross Network 问题的时候,突然悟了一下, bit-wise 最大的问题其实在于违背了特征交互的初衷, 我们本意上其实是让模型学习特征之间的交互,放到 embedding 的角度,也理应是 embedding 与 embedding 的相关作用交互, 但 bit-wise 已经没有了 embedding 的概念,以 bit 为最细粒度进行学习, 这里面既有不同 embedding 的 bit 交互,也有同一 embedding 的 bit 交互,已经意识不到 Field vector 的概念。 具体可以看 Cross Network 那里的解释,分析了 Cross Network 之后,可能会更好理解些。
这个问题最好是先这样理解或者自己思考下,因为 xDeepFM 的一个挺大的亮点就是保留了 FM 的这种 vector-wise 的特征交互模式,也是作者一直强调的,vector-wise 应该是要比 bit-wise 要好的,否则作者就不会强调 Cross Network 的弊端之一就是 bit-wise,而改进的方法就是设计了 CIN,用的是 vector-wise。
高阶隐性特征交互 (DNN) VS 高阶显性特征交互 (Cross Network)
DNN 的隐性高阶交互
DNN 非常擅长学习特征之间的高阶交互信息,但是隐性的,这个比较好理解了,前面也提到过:
但是问题的话,前面也剖析过了, 简单总结:
- DNN 是一种隐性的方式学习特征交互, 但这种交互是不可解释性的, 没法看出究竟是学习了几阶的特征交互
- DNN 是在 bit-wise 层级上学习的特征交互, 这个不同于传统的 FM 的 vector-wise
- DNN 是否能有效的学习高阶特征交互是个迷,其实不知道学习了多少重要的高阶交互,哪些高阶交互会有作用,高阶到了几阶等, 如果用的话,只能靠玄学二字来解释
Cross Network 的显性高阶交互
谈到显性高阶交互,这里就必须先分析一下我们大名鼎鼎的 DCN 网络的 Cross Network 了, 关于这个模型,我在 AI 上推荐 之 Wide&Deep 与 Deep&Cross 模型文章中进行了一些剖析,这里再复习的话我又参考了一个大佬的文章,因为再把我之前的拿过来感觉没有啥意思,重新再阅读别人的文章很可能会再 get 新的点,于是乎还真的学习到了新东西,具体链接放到了下面。 这里我们重温下 Cross Network,看看到底啥子叫显性高阶交互。再根据论文看看这样子的交互有啥问题。
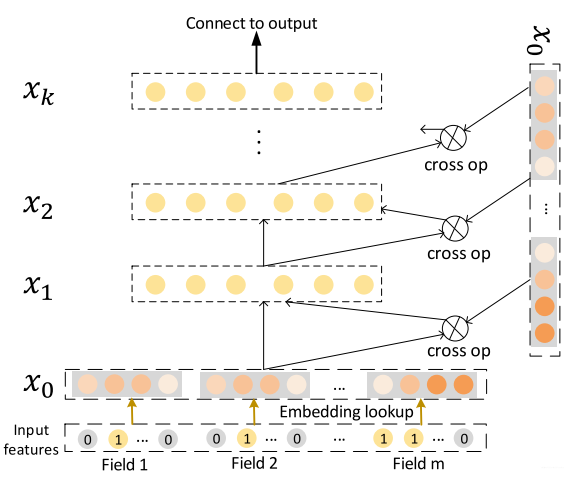
这里的输入
Cross 的目的是一一种显性、可控且高效的方式,自动构造有限高阶交叉特征。 具体的公式如下:
其中

Cross Layer 的巧妙之处全部体现在上面的公式,下面放张图是为了更好的理解,这里我们回顾一些细节。
- 每层的神经元个数相同,都等于输入
- 残差网络的结构启发,每层的函数
那么显性交叉到底体会到哪里呢? 还是拿我之前举的那个例子:假设
最后得到
- 有限高阶: 叉乘阶数由网络深度决定, 深度
- 自动叉乘:Cross 输出包含了原始从一阶 (本身) 到
- 参数共享:不同叉乘项对应的权重不同,但并非每个叉乘组合对应独立的权重,通过参数共享,Cross 有效降低了参数数量。 并且,使得模型有更强的泛化性和鲁棒性。例如,如果独立训练权重,当训练集中
这里有一点很值得留意,前面介绍过,文中将 dense 特征和 embedding 特征拼接后作为 Cross 层和 Deep 层的共同输入。这对于 Deep 层是合理的,但我们知道人工交叉特征基本是对原始 sparse 特征进行叉乘,那为何不直接用原始 sparse 特征作为 Cross 的输入呢?联系这里介绍的 Cross 设计,每层 layer 的节点数都与 Cross 的输入维度一致的,直接使用大规模高维的 sparse 特征作为输入,会导致极大地增加 Cross 的参数量。当然,可以畅想一下,其实直接拿原始 sparse 特征喂给 Cross 层,才是论文真正宣称的 “省去人工叉乘” 的更完美实现,但是现实条件不太允许。所以将高维 sparse 特征转化为低维的 embedding,再喂给 Cross,实则是一种 trade-off 的可行选择。
看下 DNN 与 Cross Network 的参数量对比:
初始输入
可以看到 Cross 的参数量随
好了, Cross 的好处啥的都分析完了, 下面得分析点不好的地方了,否则就没法引出这次的主角了。作者直接说:

每一层学习到的是
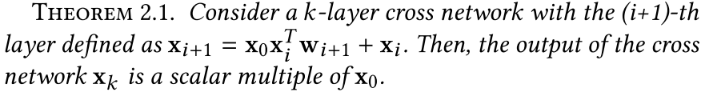
这里作者用数学归纳法进行了证明。
当
这里的
其中
所以作者认为 Cross Network 有两个缺点:
- 由于每个隐藏层是
- CrossNet 的特征交互是 bit-wise 的方式 (这个经过上面举例子应该是显然了),这种方式 embedding 向量的各个元素也会互相影响,这样在泛化能力上可能受到限制,并且也意识不到 Field Vector 的概念,这其实违背了我们特征之间相互交叉的初衷。因为我们想让模型学习的是特征与特征之间的交互或者是相关性,从 embedding 的角度,,那么自然的特征与特征之间的交互信息应该是 embedding 与 embedding 的交互信息。 但是 bit-wise 的交互上,已经意识不到 embedding 的概念了。由于最细粒度是 bit (embedding 的具体元素),所以这样的交互既包括了不同 embedding 不同元素之间的交互,也包括了同一 embedding 不同元素的交互。本质上其实发生了改变。 这也是作者为啥强调 CIN 网络是 vector-wise 的原因。而 FM,恰好是以向量为最细粒度学习相关性。
好了, 如果真正理解了 Cross Network,以及上面存在的两个问题,理解 xDeepFM 的动机就不难了,xDeepFM 的动机,正是将 FM 的 vector-wise 的思想引入到了 Cross 部分。
下面主角登场了:

xDeepFM 模型的理论以及论文细节
了解了 xDeepFM 的动机,再强调下 xDeepFM 的核心,就是提出的一个新的 Cross Network (CIN),这个是基于 DCN 的 Cross Network,但是有上面那几点好处。下面的逻辑打算是这样,首先先整体看下 xDeepFM 的模型架构,由于我们已经知道了这里其实就是用一个 CIN 网络代替了 DCN 的 Cross Network,那么这里面除了这个网络,其他的我们都熟悉。 然后我们再重点看看 CIN 网络到底在干个什么样的事情,然后再看看 CIN 与 FM 等有啥关系,最后分析下这个新网络的时间复杂度等问题。
xDeepFM 的架构剖析
首先,我们先看下 xDeepFM 的架构
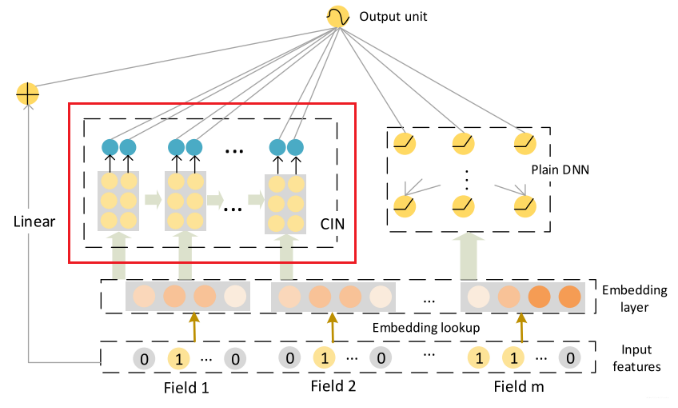
这个网络结构名副其实,依然是采用了 W&D 架构,DNN 负责 Deep 端,学习特征之间的隐性高阶交互, 而 CIN 网络负责 wide 端,学习特征之间的显性高阶交互,这样显隐性高阶交互就在这个模型里面体现的淋漓尽致了。不过这里的线性层单拿出来了。

最终的计算公式如下:
这里的
最终的目标函数加了正则化:
CIN 网络的细节 (重头戏)
这里尝试剖析下本篇论文的主角 CIN 网络,全称 Compressed Interaction Network。这个东西说白了其实也是一个网络,并不是什么高大上的东西,和 Cross Network 一样,也是一层一层,每一层都是基于一个固定的公式进行的计算,那个公式长这样:
这个公式第一眼看过来,肯定更是懵逼,这是写的个啥玩意?如果我再把 CIN 的三个核心图放上来:
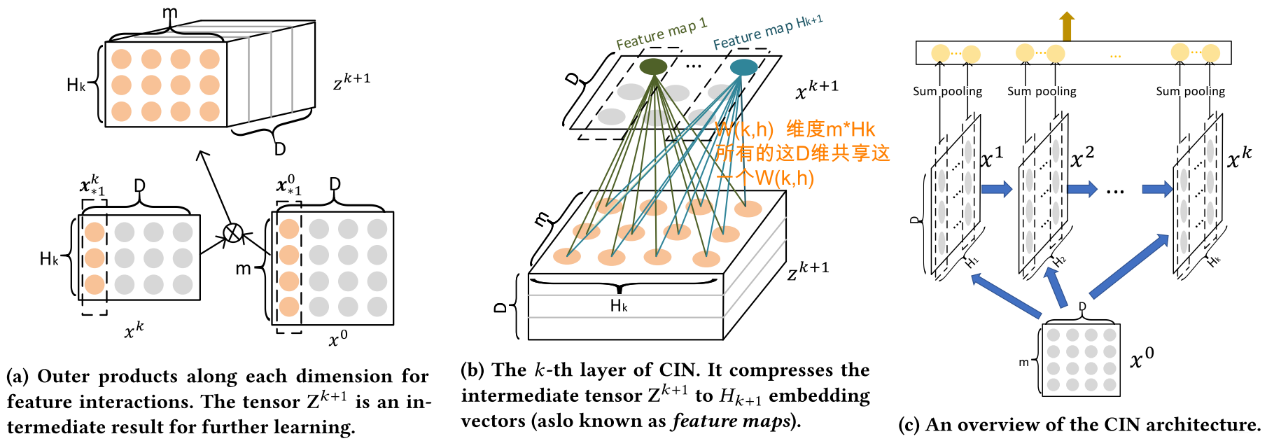
上面其实就是 CIN 网络的精髓了,也是它具体的运算过程,只不过直接上图的话,会有些抽象,难以理解,也不符合我整理论文的习惯。下面,我们就一一进行剖析, 先从上面这个公式开始。但在这之前,需要先约定一些符号。要不然不知道代表啥意思。
所以上面的那个公式:
其实就是计算第
那么这个公式到底表示的啥意思呢? 是具体怎么计算的呢?我们往前计算一层就知道了,这里令
这里的
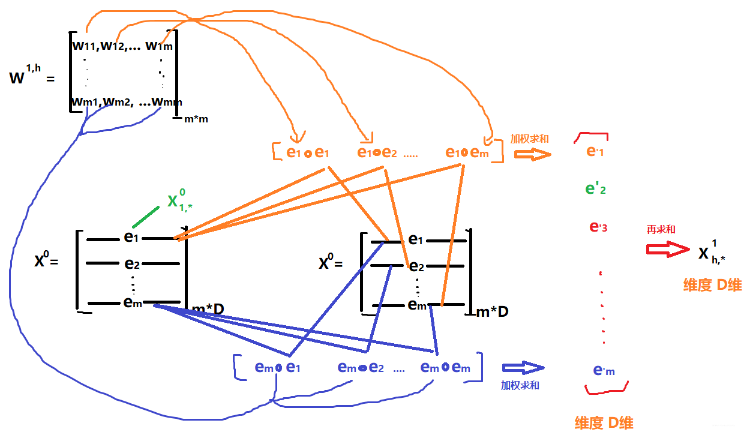
这就是上面那个公式的具体过程了,图实在是太难看了, 但应该能说明这个详细的过程了。这样只要给定一个
这个过程明白了之后,再看论文后面的内容就相对容易了,首先

CIN 里面能看到 RNN 的身影,也就是当前层的隐藏单元的计算要依赖于上一层以及当前的输入层,只不过这里的当前输入每个时间步都是
下面我们再从 CNN 的角度去看这个计算过程。其实还是和上面一样的计算过程,只不过是换了个角度看而已,所以上面那个只要能理解,下面 CNN 也容易理解了。首先,这里引入了一个 tensor 张量

这个可以看成是一个三维的图片,
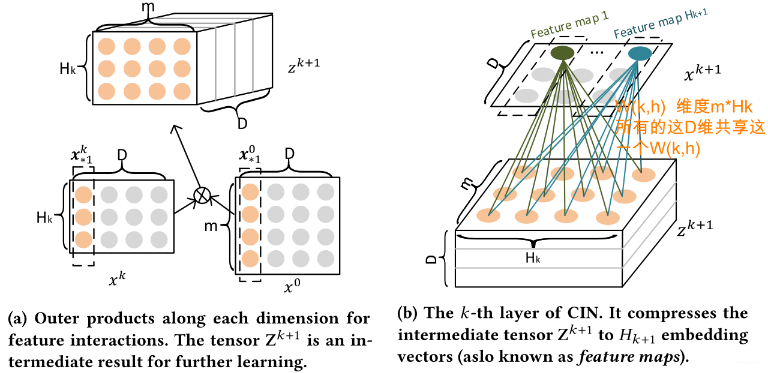
通过这样的一个 CIN 网络,就很容易的实现了特征的显性高阶交互,并且是 vector-wise 级别的,那么最终的输出层是啥呢? 通过上面的分析,首先我们了解了对于第
每一层,都会得到一个这样的向量,那么把所有的向量拼接到一块,其实就是 CIN 网络的输出了。之所以,这里要把中间结果都与输出层相连,就是因为 CIN 与 Cross 不同的一点是,在第
这也就是第三个图表示的含义:
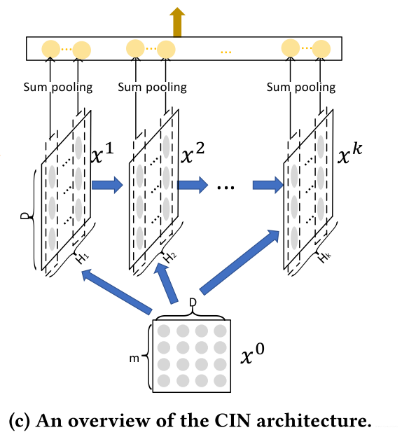
这样, 就得到了最终 CIN 的输出
后面那个维度的意思,就是说每一层是的向量维度是
CIN 网络的其他角度分析
设计意图分析
CIN 和 DCN 层的设计动机是相似的,Cross 层的 input 也是前一层与输入层,这么做的原因就是可以实现: 有限高阶交互,自动叉乘和参数共享。
但是 CIN 与 Cross 的有些地方是不一样的:
- Cross 是 bit-wise 级别的, 而 CIN 是 vector-wise 级别的
- 在第
时间和空间复杂度分析
- 空间复杂度 假设 CIN 和 DNN 每层神经元个数是
再看 DNN,第一层是
所以空间上来说,CIN 会有优势。 - 时间复杂度 对于 CIN, 我们计算某一层的某个特征向量的时候,需要前面的
对于普通的 DNN,花费时间
所以时间复杂度会是 CIN 的一大痛点。
多项式逼近
这地方没怎么看懂,大体写写吧, 通过对问题进行简化,即假设 CIN 中不同层的 feature map 的数量全部一致,均为 fields 的数量[m] 表示小于等于 m 的正整数。CIN 中的第一层的第
因此, 在第一层中通过
由于第二个
我们知道一个经典的
- 对于 CIN 来讲, 第
- CIN 的一系列特征图只需要
xDeepFM 与其他模型的关系
- 对于 xDeepFM,将 CIN 模块的层数设置为 1,feature map 数量也为 1 时,其实就是 DeepFM 的结构,因此 DeepFM 是 xDeepFM 的特殊形式,而 xDeepFM 是 DeepFM 的一般形式;
- 在 1 中的基础上,当我们再将 xDeepFM 中的 DNN 去除,并对 feature map 使用一个常数 1 形式的
sum filter,那么 xDeepFM 就退化成了 FM 形式了。
一般这种模型的改进,是基于之前模型进行的,也就是简化之后,会得到原来的模型,这样最差的结果,模型效果还是原来的,而不应该会比原来模型的表现差,这样的改进才更有说服力。
所以,既然提到了 FM,再考虑下面两个问题理解下 CIN 设计的合理性。
- 每层通过 sum pooling 对 vector 的元素加和输出,这么做的意义或者合理性?这个就是为了退化成 FM 做准备,如果 CIN 只有 1 层, 只有
- 除了第一层,中间层的基于 Vector 高阶组合有什么物理意义?回顾 FM,虽然是二阶的,但可以扩展到多阶,例如考虑三阶 FM,是对三个嵌入向量做哈达玛积乘再对得到的 vector 做 sum, CIN 基于 vector-wise 的高阶组合再 sum pooling 与之类似,这也是模型名字 "eXtreme Deep Factorization Machine (xDeepFM)" 的由来。
论文的其他重要细节
实验部分
这一块就是后面实验了,这里作者依然是抛出了三个问题,并通过实验进行了解答。
- CIN 如何学习高阶特征交互 通过提出的交叉网络,这里单独证明了这个结构要比 CrossNet,DNN 模块和 FM 模块要好
- 推荐系统中,是否需要显性和隐性的高阶特征交互都存在?

- 超参对于 xDeepFM 的影响
- 网络的深度:不用太深, CIN 网络层数大于 3,就不太好了,容易过拟合
- 每一层神经网络的单元数: 100 是比较合适的一个数值
- 激活函数: CIN 这里不用加任何的非线性激活函数,用恒等函数
这里用了三个数据集
- 公开数据集 Criteo 与 微软数据集 BingNews
- DianPing 从大众点评网整理的相关数据,收集 6 个月的 user check-in 餐厅 poi 的记录,从 check-in 餐厅周围 3km 内,按照 poi 受欢迎度抽取餐厅 poi 作为负例。根据 user 属性、poi 属性,以及 user 之前 3 家 check-in 的 poi,预测用户 check-in 一家给定 poi 的概率。
评估指标用了两个 AUC 和 Logloss, 这两个是从不同的角度去评估模型。
- AUC: AUC 度量一个正的实例比一个随机选择的负的实例排名更高的概率。它只考虑预测实例的顺序,对类的不平衡问题不敏感.
- LogLoss (交叉熵损失): 真实分数与预测分数的距离
作者说:

相关工作部分
这里作者又梳理了之前的模型,这里就再梳理一遍了
经典推荐系统
- 非因子分解模型:主要介绍了两类,一类是常见的线性模型,例如 LR with FTRL,这一块很多工作是在交互特征的特征工程方面;另一类是提升决策树模型的研究(GBDT+LR)
- 因子分解模型: MF 模型, FM 模型,以及在 FM 模型基础上的贝叶斯模型
深度学习模型
- 学习高阶交互特征:论文中提到的 DeepCross, FNN,PNN,DCN, NFM, W&D, DeepFM,
- 学习精心的表征学习:这块常见的深度学习模型不是 focus 在学习高阶特征交互关系。比如 NCF,ACF,DIN 等。
推荐系统数据特点:稀疏,类别连续特征混合,高维。
关于未来两个方向:
- CIN 的 sum pooling 这里, 后面可以考虑 DIN 的那种思路,根据当前候选商品与 embedding 的关联进行注意力权重的添加
- CIN 的时间复杂度还是比较高的,后面在 GPU 集群上使用分布式的方式来训练模型。
xDeepFM 模型的代码复现及重要结构解释
xDeepFM 的整体代码逻辑
下面看下 xDeepFM 模型的具体实现, 这样可以从更细节的角度去了解这个模型, 这里我依然是参考的 deepctr 的代码风格,这种函数式模型编程更清晰一些,当然由于时间原因,我这里目前只完成了一个 tf2 版本的 (pytorch 版本的后面有时间会补上)。 这里先看下 xDeepFM 的全貌:
def xDeepFM(linear_feature_columns, dnn_feature_columns, cin_size=[128, 128]):
# 构建输入层,即所有特征对应的Input()层,这里使用字典的形式返回,方便后续构建模型
dense_input_dict, sparse_input_dict = build_input_layers(linear_feature_columns+dnn_feature_columns)
# 构建模型的输入层,模型的输入层不能是字典的形式,应该将字典的形式转换成列表的形式
# 注意:这里实际的输入预Input层对应,是通过模型输入时候的字典数据的key与对应name的Input层
input_layers = list(dense_input_dict.values()) + list(sparse_input_dict.values())
# 线性部分的计算逻辑 -- linear
linear_logits = get_linear_logits(dense_input_dict, sparse_input_dict, linear_feature_columns)
# 构建维度为k的embedding层,这里使用字典的形式返回,方便后面搭建模型
# 线性层和dnn层统一的embedding层
embedding_layer_dict = build_embedding_layers(linear_feature_columns+dnn_feature_columns, sparse_input_dict, is_linear=False)
# DNN侧的计算逻辑 -- Deep
# 将dnn_feature_columns里面的连续特征筛选出来,并把相应的Input层拼接到一块
dnn_dense_feature_columns = list(filter(lambda x: isinstance(x, DenseFeat), dnn_feature_columns)) if dnn_feature_columns else []
dnn_dense_feature_columns = [fc.name for fc in dnn_dense_feature_columns]
dnn_concat_dense_inputs = Concatenate(axis=1)([dense_input_dict[col] for col in dnn_dense_feature_columns])
# 将dnn_feature_columns里面的离散特征筛选出来,相应的embedding层拼接到一块
dnn_sparse_kd_embed = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=True)
dnn_concat_sparse_kd_embed = Concatenate(axis=1)(dnn_sparse_kd_embed)
# DNN层的输入和输出
dnn_input = Concatenate(axis=1)([dnn_concat_dense_inputs, dnn_concat_sparse_kd_embed])
dnn_out = get_dnn_output(dnn_input)
dnn_logits = Dense(1)(dnn_out)
# CIN侧的计算逻辑, 这里使用的DNN feature里面的sparse部分,这里不要flatten
exFM_sparse_kd_embed = concat_embedding_list(dnn_feature_columns, sparse_input_dict, embedding_layer_dict, flatten=False)
exFM_input = Concatenate(axis=1)(exFM_sparse_kd_embed)
exFM_out = CIN(cin_size=cin_size)(exFM_input)
exFM_logits = Dense(1)(exFM_out)
# 三边的结果stack
stack_output = Add()([linear_logits, dnn_logits, exFM_logits])
# 输出层
output_layer = Dense(1, activation='sigmoid')(stack_output)
model = Model(input_layers, output_layer)
return model2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
这种风格最好的一点,就是很容易从宏观上把握模型的整体逻辑。 首先,接收的输入是 linear_feature_columns 和 dnn_feature_columns, 这两个是深度和宽度两侧的特征,具体选取要结合着场景来。 接下来,就是为这些特征建立相应的 Input 层,这里要分成连续特征和离散的特征,因为后面的处理方式不同, 连续特征的话可以直接拼了, 而离散特征的话,需要过一个 embedding 层转成低维稠密,这就是第一行代码干的事情了。
接下来, 计算线性部分,从上面 xDeepFM 的结构里面可以看出, 是分三路走的,线性,CIN 和 DNN 路, 所以 get_linear_logits 就是线性这部分的计算结果,完成的是
接下来是另外两路,DNN 这路也比较简单, dnn_feature_columns 里面的离散特征过 embedding,和连续特征拼接起来,然后过 DNN 即可。 CIN 这路使用的是 dnn_feature_columns 里面的离散 embedding 特征,进行显性高阶交叉,这里的输入是 [None, field_num, embedding_dim] 的维度。这个也好理解,每个特征 embedding 之后,拼起来即可,注意 flatten=False 了。 这个输入,过 CIN 网络得到输出。
这样三路输出都得到,然后进行了一个加和,再连接一个 Dense 映射到最终输出。这就是整体的逻辑了,关于每个部分的具体细节,可以看代码。 下面主要是看看 CIN 这个网络是怎么实现的,因为其他的在之前的模型里面也基本是类似的操作,比如前面 DIEN,DSIN 版本,并且我后面项目里面补充了 DCN 的 deepctr 风格版,这个和那个超级像,唯一不同的就是把 CrossNet 换成了 CIN,所以这个如果感觉看不大懂,可以先看那个网络代码。下面说 CIN。
CIN 网络的代码实现细节
再具体代码实现, 我们先简单捋一下 CIN 网络的实现过程,这里的输入是 [None, field_num embed_dim] 的维度,在 CIN 里面,我们知道接下来的话,就是每一层会有
class CIN(Layer):
def __init__(self, cin_size, l2_reg=1e-4):
"""
:param: cin_size: A list. [H_1, H_2, ....H_T], a list of number of layers
"""
super(CIN, self).__init__()
self.cin_size = cin_size
self.l2_reg = l2_reg
def build(self, input_shape):
# input_shape [None, field_nums, embedding_dim]
self.field_nums = input_shape[1]
# CIN 的每一层大小,这里加入第0层,也就是输入层H_0
self.field_nums = [self.field_nums] + self.cin_size
# 过滤器
self.cin_W = {
'CIN_W_' + str(i): self.add_weight(
name='CIN_W_' + str(i),
shape = (1, self.field_nums[0] * self.field_nums[i], self.field_nums[i+1]), # 这个大小要理解
initializer='random_uniform',
regularizer=l2(self.l2_reg),
trainable=True
)
for i in range(len(self.field_nums)-1)
}
super(CIN, self).build(input_shape)
def call(self, inputs):
# inputs [None, field_num, embed_dim]
embed_dim = inputs.shape[-1]
hidden_layers_results = [inputs]
# 从embedding的维度把张量一个个的切开,这个为了后面逐通道进行卷积,算起来好算
# 这个结果是个list, list长度是embed_dim, 每个元素维度是[None, field_nums[0], 1] field_nums[0]即输入的特征个数
# 即把输入的[None, field_num, embed_dim],切成了embed_dim个[None, field_nums[0], 1]的张量
split_X_0 = tf.split(hidden_layers_results[0], embed_dim, 2)
for idx, size in enumerate(self.cin_size):
# 这个操作和上面是同理的,也是为了逐通道卷积的时候更加方便,分割的是当一层的输入Xk-1
split_X_K = tf.split(hidden_layers_results[-1], embed_dim, 2) # embed_dim个[None, field_nums[i], 1] feild_nums[i] 当前隐藏层单元数量
# 外积的运算
out_product_res_m = tf.matmul(split_X_0, split_X_K, transpose_b=True) # [embed_dim, None, field_nums[0], field_nums[i]]
out_product_res_o = tf.reshape(out_product_res_m, shape=[embed_dim, -1, self.field_nums[0]*self.field_nums[idx]]) # 后两维合并起来
out_product_res = tf.transpose(out_product_res_o, perm=[1, 0, 2]) # [None, dim, field_nums[0]*field_nums[i]]
# 卷积运算
# 这个理解的时候每个样本相当于1张通道为1的照片 dim为宽度, field_nums[0]*field_nums[i]为长度
# 这时候的卷积核大小是field_nums[0]*field_nums[i]的, 这样一个卷积核的卷积操作相当于在dim上进行滑动,每一次滑动会得到一个数
# 这样一个卷积核之后,会得到dim个数,即得到了[None, dim, 1]的张量, 这个即当前层某个神经元的输出
# 当前层一共有field_nums[i+1]个神经元, 也就是field_nums[i+1]个卷积核,最终的这个输出维度[None, dim, field_nums[i+1]]
cur_layer_out = tf.nn.conv1d(input=out_product_res, filters=self.cin_W['CIN_W_'+str(idx)], stride=1, padding='VALID')
cur_layer_out = tf.transpose(cur_layer_out, perm=[0, 2, 1]) # [None, field_num[i+1], dim]
hidden_layers_results.append(cur_layer_out)
# 最后CIN的结果,要取每个中间层的输出,这里不要第0层的了
final_result = hidden_layers_results[1:] # 这个的维度T个[None, field_num[i], dim] T 是CIN的网络层数
# 接下来在第一维度上拼起来
result = tf.concat(final_result, axis=1) # [None, H1+H2+...HT, dim]
# 接下来, dim维度上加和,并把第三个维度1干掉
result = tf.reduce_sum(result, axis=-1, keepdims=False) # [None, H1+H2+..HT]
return result2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
这里主要是解释四点:
- 每一层的 W 的维度,是一个
[1, self.field_nums[0]*self.field_nums[i], self.field_nums[i+1]的,首先,得明白这个self.field_nums存储的是每一层的神经单元个数,这里包括了输入层,也就是第 0 层。那么每一层的每个神经元计算都会有一个 - 具体实现的时候,这里为了更方便计算,采用了切片的思路,也就是从 embedding 的维度把张量切开,这样外积的计算就会变得更加的简单。
- 具体卷积运算的时候,这里采用的是 Conv1d,1 维卷积对应的是一张张高度为 1 的图片 (理解的时候可这么理解),输入维度是
[None, in_width, in_channels]的形式,而对应这里的数据是[None, dim, field_nums[0]*field_nums[i]], 而这里的过滤器大小是[1, field_nums[0]*field_nums[i], field_nums[i+1], 这样进行卷积的话,最后一个维度是卷积核的数量。是沿着 dim 这个维度卷积,得到的是[None, dim, field_nums[i+1]]的张量,这个就是第

这个不同的是它把前面这个矩形 Flatten 了,得到了一个
关于 CIN 的代码细节解释到这里啦,剩下的可以看后面链接里面的代码了。
总结
这篇文章主要是介绍了又一个新的模型 xDeepFM, 这个模型的改进焦点依然是特征之间的交互信息,xDeepFM 的核心就是提出了一个新的 CIN 结构 (这个是重点,面试的时候也喜欢问),将基于 Field 的 vecotr-wise 思想引入到了 Cross Network 中,并保留了 Cross 高阶交互,自动叉乘,参数共享等优势,模型结构上保留了 DeepFM 的广深结构。主要有三大优势:
- CIN 可以学习高效的学习有界的高阶特征;
- xDeepFM 模型可以同时显示和隐式的学习高阶交互特征;
- 以 vector-wise 方式而不是 bit-wise 方式学习特征交互关系。
如果说 DeepFM 只是 “Deep & FM”,那么 xDeepFm 就真正做到了”Deep” Factorization Machine。当然,xDeepFM 的时间复杂度比较高,会是工业落地的主要瓶颈,后面需要进行一些优化操作。
这篇论文整体上还是非常清晰的,实验做的也非常丰富,语言描述上也非常地道,建议读读原文呀。
参考: