1.2 逻辑代数与化简
一、逻辑代数定义
- 逻辑代数(布尔代数 Boolean Algebra):用符号 0/1 表示 “假 / 真”,以有限个基本运算描述命题真假关系的代数系统。
- 真值:只有两个离散值 ——0(False)、1(True)。
- 变量:逻辑变量用大写字母 A、B、C… 表示,取值为 0 或 1。
- 函数:逻辑函数 F (A,B,…) 通过基本运算组合而成,其输出也为 0 或 1。
二、基本逻辑运算
| 运算 | 记号 | 真值表 | 逻辑门符号 | 读法 | 记忆口诀 |
|---|---|---|---|---|---|
| 与 (AND) | A・B 或 AB | 00→0, 01→0, 10→0, 11→1 | 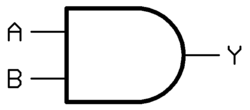 | “A 与 B” | “全 1 才 1” |
| 或 (OR) | A + B | 00→0, 01→1, 10→1, 11→1 | 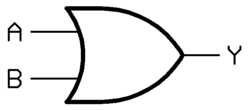 | “A 或 B” | “有 1 就 1” |
| 非 (NOT) | ¬A 或 Ā | 0→1, 1→0 | 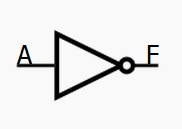 | “非 A” | “取反” |
三、复合逻辑运算
| 运算 | 定义式 | 记号 | 真值表(A,B→输出) | 逻辑门符号(图片) | 真值特征 |
|---|---|---|---|---|---|
| 与非 (NAND) | ¬(A·B) | A ↑ B | 00→1, 01→1, 10→1, 11→0 |  | 先与后非 |
| 或非 (NOR) | ¬(A+B) | A ↓ B | 00→1, 01→0, 10→0, 11→0 |  | 先或后非 |
| 与或非 (AOI) | 先与再或再非 | ¬(AB+CD) | 0000→1, 0001→1, 0010→1, 0011→0, …(16 行) | 无标准单门符号,可用 NAND/NOR 组合实现 | 复杂组合 |
| 异或 (XOR) | A·¬B + ¬A·B | A ⊕ B | 00→0, 01→1, 10→1, 11→0 |  | 不同为 1 |
| 同或 (XNOR) | ¬(A ⊕ B) | A ⊙ B | 00→1, 01→0, 10→0, 11→1 | 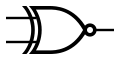 | 相同为 1 |
四、逻辑表达式化简与转换
4.1 基本定律
| 类别 | 名称 | 公式 |
|---|---|---|
| 恒等律 | 与恒等 | A·1 = A |
| 或恒等 | A+0 = A | |
| 零一律 | 与零 | A·0 = 0 |
| 或一 | A+1 = 1 | |
| 互补律 | 自补 | A·¬A = 0, A+¬A = 1 |
| 重叠律 | 与重叠 | A·A = A |
| 或重叠 | A+A = A | |
| 吸收律 | 吸收 | A+AB = A, A(A+B)=A |
| 分配律 | 与分配 | A(B+C)=AB+AC |
| 或分配 | A+BC=(A+B)(A+C) | |
| 德摩根律 | 反演 | ¬(AB)=¬A+¬B, ¬(A+B)=¬A·¬B |
4.2 化简方法
| 方法 | 步骤 | 示例 | 结果 |
|---|---|---|---|
| 代数法 | 套用定律、吸收、合并 | F = AB + A¬B + ¬AB | 吸收后 F = A + B |
| 卡诺图 | 1. 列出真值表 → 2. 填 K-map → 3. 圈 1 得最小项 → 4. 写出最简式 |  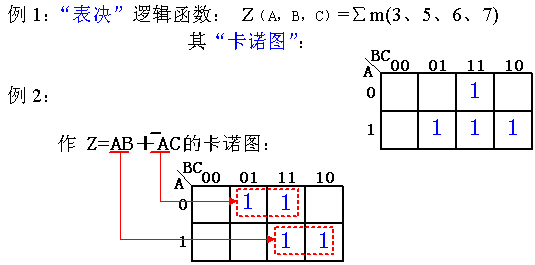 | 如左图所示 |
| 列表法 (Quine-McCluskey) | 系统化找最小项 → 合并素项 → 选最小覆盖 | 适合变量 > 4 | 同上 |
五、离散数学基础:逻辑与集合
| 概念 | 逻辑对应 | 集合对应 | 记号 |
|---|---|---|---|
| 命题 | 逻辑变量 | 元素属性 | p, q |
| 合取 | AND | 交集 | p∧q, A∩B |
| 析取 | OR | 并集 | p∨q, A∪B |
| 否定 | NOT | 补集 | ¬p, Aᶜ |
| 蕴含 | IMPLIES | 子集 | p⇒q, A⊆B |
| 等价 | ↔ | 相等 | p↔q, A=B |
| 量词 | — | — | ∀x P(x), ∃x P(x) |
德摩根律在集合中的镜像:¬(A∩B)=¬A∪¬B,¬(A∪B)=¬A∩¬B
六、速查表:常用等价式
| 原式 | 最简式 |
|---|---|
| AB + A¬B | A |
| A + ¬AB | A + B |
| (A+B)(¬A+C) | AC + ¬AB |
| A⊕B | A¬B + ¬AB |
| ¬(A⊕B) | AB + ¬A¬B |
七、小结:运算 ↔ 化简对照
| 关注点 | 基本运算 | 化简方法 | 工具 |
|---|---|---|---|
| 符号集 | 0,1 | 0,1 | 真值表、K-map |
| 运算律 | 与、或、非 | 吸收、分配、德摩根 | 代数系统 |
| 人读性 | XOR、XNOR 直观 | 最简与或式 | 卡诺图 |
| 机器性 | 门级实现 | 门级统一 | 门阵列 |
clh,
25.8.7